SPOJ Problem Set (classical) - Light switching (1st attempt)

Oct 25, 2014 divide and conquer avl tree spoj

Problem:

Please find the problem here.

Solution:

This problem is really a hard nut to crack. I know there exist simpler solution, but I am going with my idea and implement that complex idea first. The goal is, really, to prove to myself that my idea works, and that to practice coding and debugging complex algorithm.

It all started with some simple observations. Judging from the numbers, I believe we can’t allow update to take time proportional to the interval length, or otherwise one could easily construct an example to just keep flipping the whole interval and we are screwed with awful performance. This implies we are doing some sort of virtualized storage for the lights. We won’t be actually storing all the lights (or at least not update them during updates)

Second observation is that for a query, we can’t have performance proportional to the number of updates before, for then we will also have quadratic performance by having the first half updates and second half queries. That implies the updates are not stored independently, but rather in some summary form that allows one to query without going through all of them.

With that, my idea is to have an AVL tree that look like this – after updating [1, 5] and [3, 7]

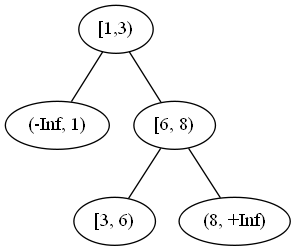
To understand that, first, let’s define elementary interval – think of all update intervals drawn on a straight line, an elementary interval is the interval between two points without any other point in between it. So in our case, it will be all the nodes.

Now, since elementary intervals never overlap, we have a natural ordering for it and we are using that for the binary search tree property. The AVL property can help us to make sure the tree is balanced and therefore the depth is at most O(log n), where n is the number of elementary intervals, which is at most twice the number of updates.

The key idea to this structure is about query. How does splitting all the input interval into elementary interval helps? It does not! The key to this structure is that we need to summarize some information on the edges.

Suppose we know in the interval [1, 3), the lights are on, in the edge from [1, 3) to [6, 8), we think of it as the edge [3, 6), there is only one elementary interval, and it is off, and is [6, 8), it is on. Then following the path from [1, 3) [3, 6), [6, 8), we can calculate the number of on lights is 2 from 2 to 6. The query time in this case will be at most O(log(n)) because that the worst case length for the path from one node to another in a balanced search tree.

The idea sounds good in theory, but in practice, but how would one implement it? Turn out implementing it is an tiring exercise that took me a good deal of time, but it has been a great practice exercise for my own sake. Once I have done with the algorithm I would also like to talk about some techniques I used to implement this, turn out it would be valuable sharing too.

A key observation that enables the implementation is that we don’t need to materialize the edge. A left edge’s information is actually the same information as the summary of the right sub-tree of the children node.

So for each node, we keep the elementary interval of course, the root to the left and right sub-trees as usual, but also the parent pointer (for query), the prev/succ pointers (for merging intervals) and balance (to maintain AVL invariant). The key summaries used is the number of finite segments, the sum of the even numbered segment lengths, and the sum of odd numbered segment lengths, summarized over both sub-trees (and itself included).

Turn out once we have decided what state the keep, the rest is easy (at least to think of). To start with, standard AVL tree operations will take care of left pointer, right pointers and balance. Prev and Succ pointers can be maintained in insertion when a new leaf node is created, its immediate parent must be either a prev or succ (depends on the new node is a leave child or not). In deletion, prev and succ pointers can be maintained easily as we can find out the prev/succ node before deletion and link them back together. All the summaries are updated whenever left or right pointer changes, and combining summary is easy.

Query is easy too, first, find out the interval containing from, the interval containing to, and the node when they start the split. Leveraging the parent pointers and split node it will be easy to find a path. Combine the summary on the way and that’s it.

All is easy to say, hard to code, that’s why it take me so long to get this completed (and that’s why I write so much that I usually don’t)

To aid implementation, the first thing I do is to introduce logging. Writing out the state explicitly make debugging easy. For example, I dump the tree to console after every operation, and that make debugging easier than it is.

Second, I use assertions. In the code, you might see unnecessary checks. For example, I check if the node is its parent’s left child, and then check if it is its parent’s right child. The second check is not necessary, but the good thing is that I add a else branch as a catch all ,and just throw an exception when that happen, now debugging is even easier because the code is now telling me what’s wrong with the data structure.

Third, to go further, I added the invariant checks. It is sometimes hard to make sure the tree is AVL, and by adding those checks every time after a tree operation, again, the code is telling me when it goes wrong.

Fourth, I added randomized testing. I generate random inputs in small sizes and generate expectation by brute force, and that happened me to find the majority of the bugs.

Fifth, you might notice the code is filled with comment, those are on purpose. With multiple days project on non-trivial algorithm, comment is essential to record what I thought. It is also essential during debugging so that I can verify the program is actually in the expected state.

All these are just general implementation techniques, but I found these particularly useful, especially so for this problem.

Unfortunately, with all these algorithmic analysis - the code still cause time limit exceed on the judge server. Guess I either need to optimize this even more (for example, to reduce allocation) or try the simpler approach (which I will).

Code: